泥板上的配方

3000年前，古巴比倫人生活於美索不達米亞平原(Mesopotamia ，現今伊拉克)。他們用削尖的蘆葦做筆，把文字刻在泥胚上，然後把泥胚烘乾，成為泥版，由於這種文字形狀成尖劈形，所以被稱為楔形文字。
1870年至今大約有五十萬塊泥板出土，楔形文字記錄了當時文明，其中有300多塊是數學文獻。1920~1950年因為法國人Thureau-Dangin和美國人O. Neugebauer的考證解讀，讓後人可以看見古巴比倫文明，也認識他們所發展的數學文化。

編號 BM13901 (西元前1800年) 的泥版上記錄一道數學題： 「正方形面積與邊長之和為$\large\frac{3}{4}$，試求邊長？」
古巴比倫人的解法和現在的配方法是一樣的，算是配方法解二次方程的濫觴。

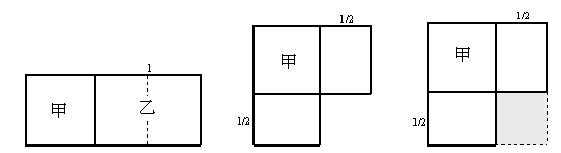
附圖，正方形甲和長方形乙等寬並且乙的長是1，已知甲和乙的面積和是$\large\frac{3}{4}$。將長方形乙沿著長的中線對切，並將其中一半和正方形甲緊貼。最後，加進一個邊長$\large\frac{1}{2}$的正方形，組成面積為1的正方形。 可解得正方形甲的邊長是 1-$\large\frac{1}{2}$ = $\large\frac{1}{2}$ 。

古巴比倫人運用幾何法解題，方法如同解二次方程的配方法。
假設正方形甲的邊長是 x，依題意可列方程式 x² + x =$\large\frac{3}{4}$，
x²+x+($\large\frac{1}{2}$)² = $\large\frac{3}{4}$+($\large\frac{1}{2}$)² = 1，
(x+$\large\frac{1}{2}$)² = 1，x +$\large\frac{1}{2}$ = 1，x = 1-$\large\frac{1}{2}$ = $\large\frac{1}{2}$。

相關網頁:古巴比倫根號 2