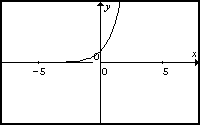懸鍊線

1682年萊布尼茲創辦《Acta eruditorum》期刊，這是歐洲德語地區的第一本科學期刊。在期刊的1690年5月號雅各·白努力寫道：「現在我正式提出以下問題：把一條細繩掛在兩個定點上，讓它自由懸垂下來，求：該細繩會構成怎樣的曲線呢？」
之前伽利略早就對這問題感到興趣，並認為這條曲線應該是拋物線，可是1646年17歲的荷蘭科學家惠更斯證明懸鍊線不是拋物線。
1961年《Acta eruditorum》刊出三個正確解答，分別由62歲的惠更斯、微積分的始創者之一的萊布尼茲、約翰各·白努力(雅各·白努力的弟弟)提出。

1748年尤拉在《無限分析引論》首先定義指數函數 e^x=$\lim_{n\to\infty} (1+\frac{x}{n})^n$，開啟常數e的濫觴。
而最早注意到雙曲函數及其跟圓函數（即三角函數）的類推關係的人是義大利數學家芮卡蒂（V.Riccati，1707～1775），他在1757年引入coshx＝$\frac{e^x+e^{-x}}{2}$，sinhx＝$\frac{e^x-e^{-x}}{2}$這兩個函數。
在微分學cosh(x)=$\large\frac{a(e^{\frac{x}{a}}+e^{\frac{-x}{a}})}{2}$的圖形就是懸鍊線，其中 a 是物理參數，包括線性密和拉住繩子的張力。聖路易斯拱門
在坐標平面上，通過兩點（x₁_，y₁）與（x₂_，y₂）的所有可能曲線，繞x軸旋轉得到旋轉體，那麼以懸鏈線所產生的旋轉體的表面積為最小。
美國密蘇里州聖路易市的地標聖路易斯拱門由建築師薩瑞能(Eero Saarinen)設計，在1965年完工。它的形狀完全和一條倒轉過來的懸鍊線一樣，其高度遠比華盛頓紀念碑、紐約自由女神像都還要高，拱門頂端高於密西西比河河岸192公尺。


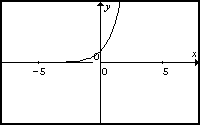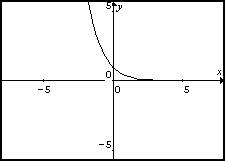
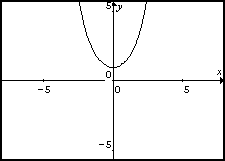
y=e^x	y=e^-x	y=$\frac{e^x+e^{-x}}{2}$

承載小雨珠的蜘蛛網、高山間高壓電塔的輸電線、美國舊金山大橋的懸索都是懸鍊線。