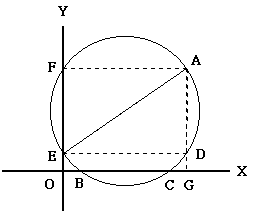
尺規作圖一元二次方程式的解

十七世紀，法國數學家笛卡兒提出以代數方程式表示幾何圖形的方法，在他創立的坐標系統中，只要知道相異兩點的坐標，便可以寫出通過這兩點的直線有理係數方程式。如果直線和圓有交點，而且已知其方程式，那麼交點的有理數坐標就可以確定。
事實上，要判斷一個幾何量是否可以尺規作圖，只需看這幾何量是否能重複有限次的運用加減乘除或平方根作圖。

以尺規作圖解一元二次方程式 x²-6x+5 = 0

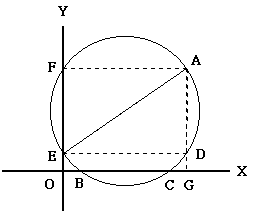
在直角坐標平面取A( 6，5 )，6是方程式的二根和，5是方程式的兩根乘積。
在Y軸上取E點，使得 OE = 1。
連接AE，再以AE為直徑作圓，分別交X軸於 B 、 C 兩點，其B點和C點的x坐標即方程式的兩根。( 為什麼 ? )

過A點作X軸的垂直線，交X軸於 G 點，並和圓交於D點。再連接DE和AF。
因為四邊形EOGD 是矩形，所以DE//BC，因此，弧BE=弧CD，即BE = CD，又OE = GD。知直角△EOB ≌ △DGC (RHS)。
所以，OB = GC。
假設 OB= a，OC = b，則 a+b = OB + OC = GC + OC = 6 。根據切割線性質知 OB×OC= OE×OF ，所以a×b=1×5 = 5。
因為 a+b = 6，ab=5。 a= 6-b，( 6 - b )b= 5，b²-6b+5=0，所以b是 x²-6x+5 = 0的根，同理 a 也是x²-6x+5 = 0的根。