正方形內相切的1/4圓和半圓

正方形ABCD內有一個以AD長為半徑所作的圓，則要如何在正方形內作一個半圓與這個圓相切，已知半圓圓心G在BC邊 ?

假設正方形ABCD的邊長是a，G點是相切半圓的圓心，其半徑是 r。

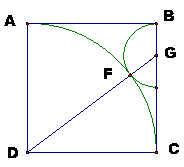
因為相切兩圓的連心線通過切點，所以D、F、G共線。
因為直角△GDC，斜邊DG= a+r，DC= a，GC= a-r。所以 (a+r)²=(a-r)²+a²，得 a= 4r，因此 GD : DC : CG = 5 : 4 : 3 ...(1)。
由(1)知，將BC四等分，第一個等分點G就是半圓的圓心，以BG當半徑在正方形內畫半圓，就可以與圓相切於F點。

命題︰「作圓D和圓G的內公切線，分別和 AB、BC 相交於 M、N 點，則△MNB~△GDC。」(為什麼?)

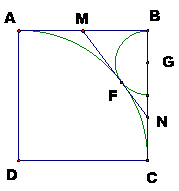
因為切線長相等，所以MA=MF，且MB=MF，得MA=MB ，因此M是AB邊的中點。
假設AB= a，則 MB=a。令NF=b，則NC=b，所以BN= a-b。
直角△MBN中，MN=MF+FN=MB+FN=a+b。又BN= a-b，MB=a，所以(a)²+(a-b)²=(a+b)²，化簡可得 a=3b。所以MN : NB : BM = 5 : 4 : 3 ...(2)。

由(1)(2)可知△GDC~△MNB(SSS)。