尺規作圖正多邊形

1798年，19歲數學家高斯發表完成尺規作圖正17邊形，並證明「如果奇數邊形的邊數是費瑪質數或是相異費瑪質數的乘積，就可以尺規作圖。」，費馬質數型如$2^{2^k}$+1，k=0、1、2、3、4。

1732年尤拉(Euler)提出F₅不是質數，F₅=4294967297=641×6700417。猜想「k＞4時，$2^{2^k}$+1都不是質數」。目前已經證明F₅~F₃₂都是合數。

「如果n是2^k或相異費瑪質數的乘積，則 n邊形可以尺規作圖。」

n = 3、4、 5 、6 、8、 10 、12 、15、16、17、 20 、24、 30、 32、34、 40、48、51、 60、64 、68、80、85、96、... ，則可以尺規作圖n邊形。

n = 7、 9、 11、 13、 14 、18 、19 、21 、22 、23、 25、 26、 27、 28 、29、 31、 33、 35、 36...，則不能尺規作圖n邊形。

尺規作圖正三邊形和正六邊形

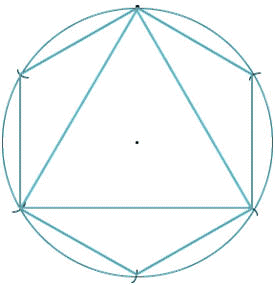
取適當長r為半徑畫圓，在圓周上任取一點，以此點為圓心，r為半徑作弧，同法再連取二個等弧，連接交點，可得正三邊形。

如果取三個等弧的中點，可以連成正六邊形。

取適當長為半徑畫圓，畫二條互相垂直的直徑，連接交點，可得正四邊形。

如果取四個等弧的中點，可以連成正八邊形。

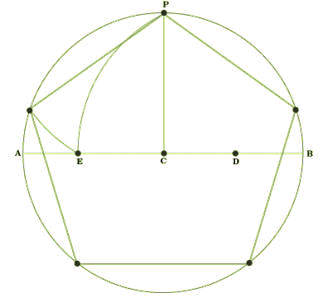
畫一圓 C。

作直徑AB。

作BC的中點D。

過C點作AB的垂直線交圓C於P點。

以D點為圓心，DP為半徑畫弧交AB於E點。

以P點為圓心，PE為半徑畫弧交圓於一點。再連續取四個等弧，連接交點，就可以作出正五邊形。

假設圓的半徑 r，圓內接正五邊形的邊長 a，則 a²=r²+r²-2×r×r×cos72°=2r²(1-$\frac{\sqrt{5}-1}{4}$)=$\frac{5-\sqrt{5}}{2}$r²，得 a=$\frac{\sqrt{10-2\sqrt{5}}}{2}$r。

證明：CP= r，取CD=$\frac{1}{2}$r，因此PD=$\frac{\sqrt{5}}{2}$r。

因為DE=PD 且 CE=DE-CD=$\frac{\sqrt{5}}{2}$r-$\frac{1}{2}$r=$\frac{\sqrt{5}-1}{2}$r，

所以 PE=$\sqrt{(\frac{\sqrt{5}-1}{2})^2+1^2}$r = $\frac{\sqrt{10-2\sqrt{5}}}{2}$r 。