四角數與畢氏定理

四角數與畢氏數

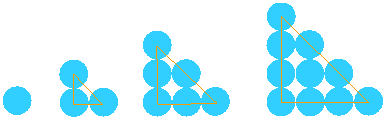
畢達歌拉斯學派的學生玩石頭排列凸多邊形，研究三角數、四角數、...等多角數，其中三角數是1，3，6，10，15，21，....，第n個三角數可以排列石頭如下圖，計算石頭數得第n個三角數=1+2+3+4+......+n=$\frac{n(n+1)}{2}$，

四角數是1，4，9，16，25，....，第n個四角數是n²。

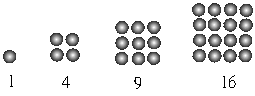
發現第n個三角數與第(n+1)個三角數相加等於第(n+1)個四角數。

可是第n個四角數與第(n+1)個四角數相加結果卻不等於第(n+2)個四角數，那麼是否存在二個相異四角數相加結果還是四角數嗎?

下圖，四角數n²，再加( 2n+1 )，得一個新的四角數( n+1)²，也就是說n²+(2n+1)=(n+1)²。

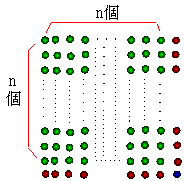
我們的問題變成是否能找出一個四角數是2n+1。

假設這個四角數是m²，即 m²=2n+1， m²是奇數，因此m²可能是9、25、49、81、....、(2k+1)²，其中k是正整數。
4²+9=5²，12²+25=13²，24²+49=25²。
這些算式等同4²+3²=5²，12²+5²=13²，24²+7²=25²，其中(4,3,5)、(12,5,13)、(24,7,25)就是畢氏數組。