更新日期：

 

| 新增素材 | 數學燈謎 | GeoGebra | 笑話數學 | 中小學科展 | 微教學動畫 |

 

 

■ 臺北市113學年度國小學教師甄選初試基礎類科知能試題第57題

 

■ 圖示配方法

■ 直觀梯形的中線性質

■ 導圓面積公式 (6年級)

■ 地震規模

■ 台北和昆明相距多遠

■ 趕鴨子過橋

■ 劃分世界時區

■ 平面鏡成像 (線對稱)

■ 機率質量函數

■ 機率樹狀圖和二項式定理

■ 硬幣試驗初識大數定律和中央極限定理

■ $\small\underbrace{3333\dots33}_{n個3}\times\underbrace{3333\dots34}_{(n-1)個3} =\small\underbrace{1111\dots11}_{n個1}\underbrace{2222\dots22}_{n個2}$  ...〈閱讀本文〉

■ 95%信賴區間

■ 拉格朗日插值法

■ 尤拉公式推導三角函數和差公式

■ 棣美弗公式推導三角函數倍角、半角公式 

 

 

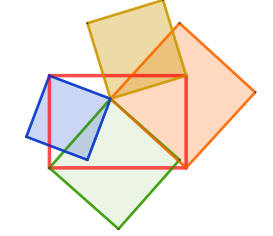
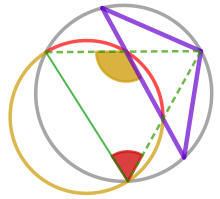
 四個正方形面積的關係   圓內接四邊形對角互補的應用




  
     
   全球網搜尋 Google  昌爸網內搜尋

    

■ 113年大學學測數學A第17題

■ 113年國中會考數學非選擇題(2)

■ 疫苗效力 (112年數學會考非選擇題第一題)

■ 111年學測數學A(18~19)
■ 111年學測數學A(20a)  /  111年學測數學A(20b) 

----------------------------------------------------------

小學數學實作

■ 用三角板畫三角形的高 ( 5年級 )

■ 利用三角板畫垂直線 ( 4年級 )

■ 用三角板畫平行四邊形的高( 5年級 )

■ 操作拼湊平行四邊形導梯形的面積公式 (5年級)

 ----------------------------------------------------------------------------------

■ 三角形預警標誌牌反光區的面積

■ 地下停車場限定高度

■ 鉛垂雨刷掃過的面積(弧)

■ 擲筊--統計圖

■  球體 ( 5年級 )
■  速度  ( 6年級 )

■ 按比例分配馬匹談分數拆分   $\frac{1}{2}+\frac{1}{3}+\frac{1}{7}+\frac{1}{42}=$1

■ 圓內接(外切)正多邊形周長逼近圓周長估計圓周率

■ 割圓術求圓周率的近似值

■ 怎麼計算教育會考的數學科加權分數

■ 誰搭不上火車 (時刻加減)

■ 搭北捷用常客優惠或買月票

■ 數字鍵盤上的秘密(11的倍數)

■ 連續綜合除法的運用 (10年級) 

■ 三次函數f(x)=a(x-h)3+p(x-h)圖形的特徵 (10年級)

 
圓周上一點到圓內接正三角形
三頂點距離的關係		 Van Schooten's Theorem

E-mail 聯絡昌爸(李信昌)

 

Copyright © 昌爸工作坊(數學網站) All Rights Reserved.